3. Trigonometry
d. Trig Identities
We now start to investigate trig identities. The first group of these are the Pythagorean Identities.
1. Pythagorean Identities
Pythagorean Theorem
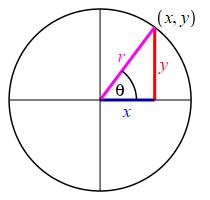
In terms of the circle which is used to define the trig functions, the Pythagorean Theorem says: \[ x^2+y^2=r^2 \qquad \text{(1)} \] \(\Leftarrow\Leftarrow\) Read it! It's fun.
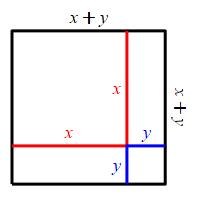
Here are two diagrams of a square with side \(x+y\).
 \(\)
\(\)
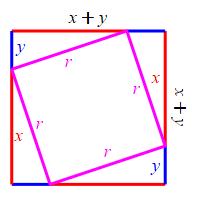
In the first, there is a square of side \(x\), a square of side \(y\) and two rectangles with sides \(x\) and \(y\). In the second, there is a square of side \(r\) and four right triangles with legs \(x\) and \(y\). We equate areas: \[ x^2+y^2+2xy=r^2+4\left(\dfrac{1}{2}xy\right) \] Cancelling \(2xy\) leaves: \[ x^2+y^2=r^2 \]
Pythagorean Identity for Sine and Cosine
\[ \sin^2\theta+\cos^2\theta=1 \qquad \text{(2)} \] \(\Leftarrow\Leftarrow\) Read it! It's easy.
Start with equation (1) and divide both sides by \(r^2\): \[ \left(\dfrac{x}{r}\right)^2+\left(\dfrac{y}{r}\right)^2=1 \] Then make the substitutions \(\dfrac{x}{r}=\cos\theta\) and \(\dfrac{y}{r}=\sin\theta\).
Pythagorean Identity for Tangent and Secant
\[ \tan^2\theta+1=\sec^2\theta \] \(\Leftarrow\Leftarrow\) Read it! It's easy.
Start with equation (2) and divide both sides by \(\cos^2\theta\): \[ \dfrac{\sin^2\theta}{\cos^2\theta}+\dfrac{\cos^2\theta}{\cos^2\theta} =\dfrac{1}{\cos^2\theta} \] Then make the substitutions \(\dfrac{\sin\theta}{\cos\theta}=\tan\theta\) and \(\dfrac{1}{\cos\theta}=\sec\theta\).
Pythagorean Identity for Cotangent and Cosecant
\[ 1+\cot^2\theta=\csc^2\theta \] \(\Leftarrow\Leftarrow\) Read it! It's easy.
Start with equation (2) and divide both sides by \(\sin^2\theta\): \[ \dfrac{\sin^2\theta}{\sin^2\theta}+\dfrac{\cos^2\theta}{\sin^2\theta} =\dfrac{1}{\sin^2\theta} \] Then make the substitutions \(\dfrac{\cos\theta}{\sin\theta}=\cot\theta\) and \(\dfrac{1}{\sin\theta}=\csc\theta\).
Consider an angle \(\alpha\) in the first quadrant for which \(\cos\alpha=0.8\). Find the other \(5\) trig functions.
Since \(\alpha\) is in the first quadrant, all the trig functions are positive. By the Pythagorean Identity, we know that \(\sin^2\alpha+\cos^2\alpha=1\). Rearranging, we see that \[\begin{aligned} \sin\alpha&=\sqrt{1-\cos^2\alpha} =\sqrt{1-0.8^2} \\ &=\sqrt{1-0.64}=\sqrt{0.36}=0.6 \end{aligned}\] We use identities for the other four trig functions: \[\begin{aligned} \tan\alpha&=\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{0.6}{0.8}=0.75 \\ \cot\alpha&=\dfrac{1}{\tan\alpha}=\dfrac{1}{0.75}=1.33\bar3 \\ \sec\alpha&=\dfrac{1}{\cos\alpha}=\dfrac{1}{0.8}=1.25 \\ \csc\alpha&=\dfrac{1}{\sin\alpha}=\dfrac{1}{0.6}=1.66\bar6 \end{aligned}\]
Consider an angle \(\beta\) in the first quadrant for which \(\sin\beta=0.96\). Find the other \(5\) trig functions.
\[\begin{aligned} &\sin\beta=\dfrac{24}{25} \quad &\cos\beta=\dfrac{7}{25} \\[8pt] &\tan\beta=\dfrac{24}{7}\quad &\cot\beta=\dfrac{7}{24} \\[8pt] &\sec\beta=\dfrac{25}{7}\quad &\csc\beta=\dfrac{25}{24} \end{aligned}\]
Since \(\beta\) is in the first quadrant, all the trig functions are positive. By the Pythagorean Identity, we know that \(\sin^2\beta+\cos^2\beta=1\). Rearranging, we see that \[ \cos\beta=\sqrt{1-\sin^2\beta} =\sqrt{1-0.9216}=\sqrt{0.0784}=0.28 \] We use identities for the other four trig functions: \[\begin{aligned} \tan\beta&=\dfrac{\sin\beta}{\cos\beta}=\dfrac{0.96}{0.28}=\dfrac{24}{7} \\ \cot\beta&=\dfrac{1}{\tan\beta}=\dfrac{1}{\dfrac{24}{7}}=\dfrac{7}{24} \\ \sec\beta&=\dfrac{1}{\cos\beta}=\dfrac{1}{0.28}=\dfrac{25}{7} \\ \csc\beta&=\dfrac{1}{\sin\beta}=\dfrac{1}{0.96}=\dfrac{25}{24} \end{aligned}\] Note: We also have: \[ \sin\beta=0.96=\dfrac{24}{25} \quad \text{and} \quad \cos\beta=0.28=\dfrac{7}{25} \]
cj
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum